Законы распределения являются одним из фундаментальных концептов статистики и вероятности. Они описывают, как вероятность того или иного значения случайной величины распределена по всем возможным значениям. Законы распределения помогают проводить анализ данных, моделирование случайных явлений и прогнозирование вероятностей.
Основными понятиями в теории вероятности и статистике являются плотность вероятности, функция распределения и случайная величина. Плотность вероятности описывает вероятность того, что случайная величина примет определенное значение. Функция распределения определяет вероятность того, что случайная величина примет значение меньшее или равное заданному. Случайная величина представляет собой величину, которая может принять различные значения с определенными вероятностями.
Существует множество различных законов распределения, каждый из которых характеризуется определенными свойствами. Некоторые из наиболее распространенных законов распределения включают нормальное распределение, равномерное распределение, биномиальное распределение, пуассоновское распределение и другие. Каждый из этих законов имеет свои уникальные особенности, и их выбор зависит от конкретной задачи и данных, с которыми вы работаете.
Понятие закона распределения
Закон распределения описывает, как вероятность различных значений случайной величины распределена между всеми возможными значениями. Вероятности, описывающие закон распределения, могут быть представлены в виде чисел или графиков.
Известные примеры законов распределения включают нормальное распределение, равномерное распределение, показательное распределение и многие другие. Каждый из этих законов описывает распределение вероятностей для различных типов случайных величин.
Общая характеристика
Законы распределения включают в себя разные вероятностные распределения, такие как равномерное распределение, нормальное распределение, биномиальное распределение и другие. Каждый из этих законов имеет свои особенности и применяется в различных областях, в зависимости от задачи, которую необходимо решить.
Равномерное распределение характеризует случайные величины, которые равновероятно принимают значения из некоторого интервала. Оно широко используется в моделировании случайных процессов.
Нормальное распределение или гауссово распределение – одно из наиболее важных и широко используемых вероятностных распределений. Оно характеризуется симметричной формой кривой и позволяет описать многие естественные и социальные явления.
Биномиальное распределение применяется в задачах, связанных с подсчетом числа успехов в серии независимых испытаний с двумя исходами. Оно находит применение в статистике, экспериментальной биологии и других областях.
Знание законов распределения позволяет проводить анализ данных, строить вероятностные модели и прогнозировать результаты случайных экспериментов. Понимание характеристик каждого закона и способов их применения особенно важно для исследователей, статистиков и специалистов в области анализа данных.
Виды законов распределения
Вероятностный закон распределения определяет вероятности появления различных значений случайной величины. Существуют различные виды законов распределения, каждый из которых описывает свои особенности и применяется в различных областях. Ниже приведены некоторые из наиболее распространенных видов законов распределения.
Нормальное распределение
Нормальное распределение, или распределение Гаусса, является одним из самых известных и важных видов законов распределения. Оно характеризуется колоколообразной формой и симметричностью относительно среднего значения. Многие случайные величины, такие как рост людей или ошибка измерения, подчиняются нормальному распределению.
Биномиальное распределение
Биномиальное распределение описывает случаи, когда существует два возможных исхода, независимых друг от друга, и вероятность каждого исхода постоянна и не меняется в ходе серии испытаний. Примерами могут служить подбрасывание монеты или бросание кости.
Равномерное распределение
Равномерное распределение характеризуется равной вероятностью появления любого значения случайной величины в определенном интервале. Например, при подбрасывании идеальной монеты вероятность выпадения герба и решки одинакова.
Экспоненциальное распределение
Экспоненциальное распределение применяется для моделирования случайных величин с экспоненциально убывающей функцией плотности вероятности. Это распределение широко применяется в физике, экономике, биологии и других областях.
Это лишь несколько примеров из богатого мира различных видов законов распределения. В каждом конкретном случае выбор подходящего закона распределения зависит от целей и особенностей исследования.
Нормальное распределение
Нормальное распределение характеризуется симметричной колоколообразной формой. Оно определяется двумя параметрами: средним значением (μ) и стандартным отклонением (σ). Среднее значение определяет положение центра распределения, а стандартное отклонение — его ширину.
Главное свойство нормального распределения — его симметричность относительно среднего значения. Вероятность попадания наблюдаемого значения в заданный интервал определяется площадью под кривой нормального распределения в этом интервале.
Центральная предельная теорема говорит, что сумма большого количества независимых одинаково распределенных случайных величин имеет нормальное распределение при некоторых условиях.
Нормальное распределение играет важную роль в статистических методах, таких как t-тест, z-тест, анализ дисперсии и регрессионный анализ. Оно также используется в практических задачах, например, для моделирования случайных процессов и прогнозирования поведения систем.
Описание и характеристики
Описание и характеристики законов распределения играют важную роль в статистике и вероятности. Эти законы описывают, как вероятность распределена для разных значений случайной величины.
Один из наиболее известных законов распределения — это нормальное (или гауссово) распределение. Оно характеризуется симметрией вокруг среднего значения и колоколообразной формой кривой. Нормальное распределение используется для моделирования различных феноменов в природе, таких как рост людей или результаты тестирования.
Еще один важный закон распределения — это равномерное распределение. В этом случае, вероятность равномерно распределена между определенными значениями случайной величины. Равномерное распределение используется, когда все значения имеют одинаковую вероятность выпадения, например, при броске справедливой монеты или при равновероятном выборе из конечного множества элементов.
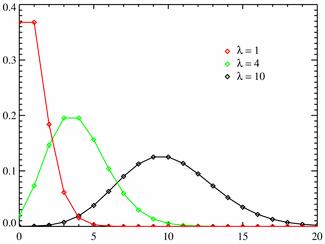
Распределение Пуассона — еще один из законов распределения, используемых для моделирования случайных событий. Оно используется для описания количества редких событий, которые происходят в случайный промежуток времени или пространства. Такое распределение может быть использовано, например, для моделирования числа звонков в кол-центре или числа аварий на дороге в определенный промежуток времени.
Это только некоторые из наиболее распространенных законов распределения. Каждый закон имеет свои уникальные характеристики, такие как форма кривой, среднее значение, дисперсия и вероятность возникновения различных значений. Знание законов распределения позволяет ученым и исследователям создавать математические модели для предсказания и анализа различных случайных явлений.
Примеры применения
Законы распределения находят широкое применение в различных областях науки, экономики и социологии. Вот несколько примеров, где они играют важную роль:
- Финансовые рынки: Законы распределения используются для моделирования колебаний цен акций, валют и других финансовых инструментов. Например, нормальное распределение (закон Гаусса) широко применяется для моделирования изменений цен акций на бирже.
- Медицина: Законы распределения используются для анализа статистических данных в медицинских исследованиях. Например, экспоненциальное распределение может быть применено для моделирования времени жизни клеток или прогнозирования времени до наступления события, такого как возникновение заболевания.
- Телекоммуникации: Законы распределения используются для анализа и оптимизации трафика в сетях связи. Например, распределение Пуассона может использоваться для моделирования количества звонков, поступающих в контакт-центр, или числа запросов к серверу.
- Социология: Законы распределения используются для изучения различных явлений в обществе. Например, распределение степени связности в социальных сетях может быть описано с использованием степенного распределения.
- Экономика: Законы распределения используются для анализа различных экономических явлений. Например, распределение Лапласа может быть использовано для моделирования колебаний цен товаров в результате маркетинговых акций.
Это лишь небольшая часть областей, где законы распределения находят применение. Они помогают ученым и специалистам получить представление о возможных исходах и вероятностях событий, что может быть полезным при принятии решений и разработке стратегии в различных сферах деятельности.
Биномиальное распределение
Биномиальное распределение определяется двумя параметрами: n – количество независимых испытаний, и p – вероятность успеха в одном испытании.
Функция вероятности биномиального распределения задается формулой:
| Количество успехов (k) | Вероятность (P(X=k)) |
|---|---|
| 0 | (1-p)^n |
| 1 | p*(1-p)^(n-1) |
| 2 | p^2*(1-p)^(n-2) |
| … | … |
| n | p^n |
Используя биномиальное распределение, можно решать множество задач, связанных с вероятностью успеха или неудачи в серии независимых экспериментов. Например, вы можете рассчитать вероятность, что при 10 бросках монеты, орел выпадет ровно 5 раз.
Биномиальное распределение имеет несколько важных свойств. Например, математическое ожидание распределения равно n*p, а дисперсия равна n*p*(1-p).
Описание и характеристики
Каждый закон распределения имеет свои уникальные характеристики, которые указывают на его форму, центральную тенденцию и разброс данных. Некоторые из основных характеристик законов распределения включают:
- Среднее значение (или математическое ожидание) — это сумма всех значений, умноженных на их вероятности, и представляет собой центральную тенденцию распределения. Обозначается символом μ.
- Дисперсия — это мера разброса значений случайной величины относительно ее среднего значения. Она вычисляется как среднее значение квадратов отклонений от среднего значения. Обозначается символом σ^2.
- Стандартное отклонение — это положительный корень из дисперсии и представляет собой меру разброса значений случайной величины. Обозначается символом σ.
- Функция плотности вероятности (density function) — это функция, которая описывает степень вероятности появления определенного значения в заданном интервале. Вероятность попасть в конкретное значение определяется как площадь под кривой функции плотности вероятности.
Законы распределения широко используются в статистике, экономике, физике, биологии и других науках для анализа данных и прогнозирования случайных явлений. Понимание и исследование различных законов распределения позволяет более точно моделировать и предсказывать различные случайные процессы.
Вопрос-ответ:
Какие основные понятия являются ключевыми при изучении законов распределения?
Основными понятиями при изучении законов распределения являются случайная величина, функция распределения, плотность распределения, математическое ожидание и дисперсия.
Что представляет собой функция распределения?
Функция распределения (CDF) — это функция, которая характеризует вероятность того, что случайная величина X меньше или равна определенному значению x. Она позволяет определить вероятности различных исходов случайного эксперимента.
В чем разница между дискретными и непрерывными распределениями?
Дискретные распределения относятся к случайным величинам, которые могут принимать только отдельные значения, тогда как непрерывные распределения относятся к случайным величинам, которые могут принимать любое значение из некоторого интервала на числовой оси.
Каким свойствам подчиняется нормальное распределение?
Нормальное распределение обладает несколькими свойствами: оно является симметричным, среднее значение, медиана и мода совпадают, оно имеет колоколообразную форму, и 68% значений случайной величины находятся в пределах одного стандартного отклонения от среднего.
Можно ли привести пример реального явления, которое можно описать распределением Пуассона?
Да, можно привести пример реального явления, описываемого распределением Пуассона — это количество звонков, поступающих в колл-центр за определенный промежуток времени. Вероятность того, что за минуту поступит определенное количество звонков, можно описать с помощью распределения Пуассона.