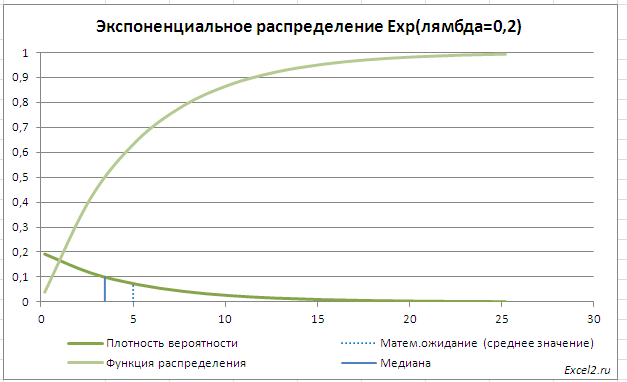
Экспоненциальное распределение является одним из основных законов распределения в теории вероятностей и статистике. Оно описывает случайную величину, время между последовательными событиями, которые происходят независимо друг от друга. Этот закон имеет множество применений в различных областях, включая математическую статистику, теорию массового обслуживания, теорию надежности и другие.
В экспоненциальном распределении случайной величине присваивается неотрицательное значение, которое описывает время между событиями. Основное свойство этого распределения заключается в том, что оно является непрерывным и имеет показательную плотность вероятности.
Одной из важных особенностей экспоненциального распределения является то, что оно не имеет памяти. То есть, вероятность наступления события не зависит от прошлых событий. Например, если случайная величина представляет время между отказами оборудования, то вероятность отказа в каждый момент времени будет одинакова, независимо от того, сколько времени оборудование уже работает.
Примером использования экспоненциального распределения может служить моделирование времени между покупками в интернет-магазине. В данном случае, случайная величина представляет время между покупками клиентами. Зная параметр распределения, можно предсказывать, сколько времени пройдет до следующей покупки и планировать соответствующие маркетинговые активности.
Особенности экспоненциального закона распределения
- Экспоненциальное распределение описывает время между событиями, которые происходят постоянно и независимо друг от друга. Например, время между приходом двух автобусов на автобусную остановку.
- Вероятность того, что событие произойдет в ближайшее время или в заданный промежуток времени, убывает экспоненциально. Это означает, что вероятность того, что событие произойдет позже, будет меньше, чем вероятность того, что оно произойдет раньше.
- Экспоненциальное распределение имеет только один параметр — среднее время между событиями, обозначаемое как λ (лямбда). Чем меньше значение λ, тем чаще события происходят, а вероятность их близкого следования выше.
- В применении экспоненциального распределения можно рассмотреть такие области, как теория надежности, телекоммуникации, физика элементарных частиц, экономика и другие. Например, в телекоммуникационных системах экспоненциальное распределение может быть использовано для моделирования времени, которое требуется для передачи данных между устройствами.
- Следует отметить, что экспоненциальное распределение предполагает, что события происходят независимо друг от друга и что время между ними имеет постоянное среднее значение. В реальности эти условия не всегда выполняются, что может привести к небольшим расхождениям между теоретическими ожиданиями и практическими наблюдениями.
Экспоненциальный закон распределения является важной моделью для анализа и прогнозирования случайных событий. Понимание его особенностей и применение позволяет эффективно решать задачи статистического моделирования и оптимизации систем и процессов.
Что такое экспоненциальный закон распределения
В экспоненциальном законе распределения вероятность наступления события за заданное время t рассчитывается по формуле:
| Функция плотности вероятности | Функция распределения |
|---|---|
| λe-λt где λ — параметр интенсивности процесса, t — время | 1 — e-λt где λ — параметр интенсивности процесса, t — время |
Особенностью экспоненциального закона распределения является то, что он является безпамятным распределением, то есть вероятность наступления события зависит только от текущего времени, а не от прошлых событий.
Примерами применения экспоненциального закона распределения являются:
- Моделирование времени между отказами системы;
- Анализ длительности жизни изделий;
- Оценка времени обслуживания клиентов;
- Прогнозирование времени ожидания процессов.
В сумме, экспоненциальный закон распределения является мощным инструментом для моделирования временных интервалов между событиями, позволяя описывать различные процессы и прогнозировать их характеристики.
Определение и формула
Формула экспоненциального закона распределения выглядит следующим образом:
f(x) = λ * e-λx
где:
- f(x) — плотность вероятности величины x;
- λ — параметр распределения, называемый интенсивностью или средней величиной события (λ > 0);
- e — константа Эйлера, приближенное значение которой равно 2,71828;
- x — случайная величина, принимающая значения на полуинтервале от 0 до плюс бесконечности.
Эта формула позволяет определять вероятности различных событий и исследовать их характеристики, такие как математическое ожидание, дисперсия и моменты различных порядков.
Примеры применения
| Область применения | Пример |
|---|---|
| Технические системы | Экспоненциальное распределение используется для моделирования времени отказа технических систем. Например, оно может быть применено для определения вероятности отказа компонентов в электронных приборах или автоматических системах. |
| Статистика | В статистике экспоненциальное распределение используется для описания времени между двумя последовательными событиями, такими как время между приходом сообщений в системе или время между двумя последовательными отказами. |
| Финансы | Экспоненциальное распределение может быть использовано для моделирования времени до наступления события, таких как время до погашения долга или время до получения прибыли в инвестиционном портфеле. |
| Телекоммуникации | В телекоммуникационных сетях экспоненциальное распределение может быть применено для моделирования времени между последовательными запросами или времени до поступления нового звонка. |
Это лишь некоторые примеры применения экспоненциального закона распределения. Его гибкость и универсальность позволяют использовать его в различных областях, где необходимо описать случайные величины, зависящие от времени или других факторов.
Примеры экспоненциального распределения
Экспоненциальное распределение широко применяется в различных областях науки, инженерии и статистике. Рассмотрим несколько примеров, где это распределение находит свое применение.
1. Время между поступлением заявок в информационную систему. Если время между поступлением заявок в систему подчиняется экспоненциальному распределению, то можно прогнозировать количество заявок, которые поступят в будущем.
2. Время между отказами оборудования. Если время между отказами оборудования имеет экспоненциальное распределение, то можно предсказать, сколько времени пройдет до следующего отказа и планировать техническое обслуживание.
3. Время между приходом посетителей в магазин или на веб-сайт. Экспоненциальное распределение может быть использовано для анализа входящего трафика и планирования ресурсов для его обработки.
4. Время ожидания в очереди. Если время ожидания в очереди подчиняется экспоненциальному распределению, то можно оптимизировать количество касс или операторов, чтобы минимизировать время ожидания клиентов.
Это лишь несколько примеров, и на самом деле экспоненциальное распределение может быть использовано во многих других сферах. Его особенности и простота использования делают его полезным инструментом для моделирования случайных событий и прогнозирования будущих значений.
Экспоненциальное распределение в технологии
- Сетевые технологии: В сетевых технологиях, таких как передача данных в компьютерных сетях или обработка сигналов в телекоммуникационных системах, важную роль играет моделирование временных задержек. Экспоненциальное распределение позволяет описать случайные задержки и предсказать их среднее время ожидания.
- Информационная безопасность: В области информационной безопасности экспоненциальное распределение помогает моделировать время жизни различных систем или алгоритмов шифрования. Это позволяет оценивать стойкость системы к взлому, предсказывать время, за которое злоумышленник может получить доступ к данным, и принимать соответствующие меры по улучшению безопасности.
- Электронная коммерция: В электронной коммерции экспоненциальное распределение может быть использовано для моделирования времени между покупками или действиями пользователей. Это позволяет предсказывать и анализировать поведение клиентов, прогнозировать спрос, оптимизировать системы рекомендаций и улучшить процессы продаж.
Это лишь несколько примеров применения экспоненциального распределения в технологии. В реальности его использование охватывает множество других областей, включая бизнес-аналитику, управление проектами, тестирование программного обеспечения и т.д. Знание и понимание этого распределения помогает создавать более эффективные и надежные системы, улучшать процессы и принимать обоснованные решения в технологической сфере.
Экспоненциальное распределение в экономике
В экономической области экспоненциальное распределение широко применяется для анализа времени между приходом клиентов, времени между событиями ремонтов и отказов оборудования, времени между обращениями клиентов к кассе и многих других процессов.
Экспоненциальное распределение обладает несколькими свойствами, которые делают его полезным в экономических моделях. Во-первых, оно имеет безпамятное свойство, что означает, что время ожидания до следующего события не зависит от времени, прошедшего с момента последнего события. Это свойство позволяет использовать экспоненциальное распределение для моделирования процессов, которые не зависят от прошлых событий.
Во-вторых, экспоненциальное распределение обладает экспоненциальным законом убывания вероятности, что означает, что вероятность того, что следующее событие произойдет через определенный промежуток времени, убывает экспоненциально с увеличением этого времени. Это позволяет использовать экспоненциальное распределение для прогнозирования вероятности поступления новых клиентов или событий в будущем на основе предшествующей информации.
Важно отметить, что использование экспоненциального распределения в экономических моделях требует предварительного исследования и адаптации к конкретной ситуации. Размер выборки, методы сбора данных и другие факторы могут влиять на точность модели и результаты анализа.
Тем не менее, экспоненциальное распределение остается полезным и мощным инструментом для моделирования времени между событиями в экономике, и его применение может привести к более точным прогнозам и принятию обоснованных решений на основе статистических данных.
Вопрос-ответ:
Что такое экспоненциальный закон распределения?
Экспоненциальный закон распределения — это математическая модель, которая описывает вероятность наступления событий с постоянной интенсивностью и без памяти. Он является основным распределением для моделирования времени между наступлением событий в различных областях, таких как теория вероятностей, теория надежности, экономика и другие.
Какова формула экспоненциального закона распределения?
Формула экспоненциального закона распределения выглядит следующим образом: f(x) = λ * e^(-λx), где λ — интенсивность событий, а x — время между наступлением событий. При этом x должно быть неотрицательным.
Какие особенности имеет экспоненциальный закон распределения?
Основные особенности экспоненциального закона распределения включают постоянную интенсивность событий, отсутствие памяти (т.е. события не зависят от предыдущих) и положительность времени между наступлением событий. Этот закон также имеет множество приложений, таких как моделирование времени между отказами оборудования, времени ожидания в очередях и др.
Можете привести примеры, где используется экспоненциальный закон распределения?
Конечно! Примеры использования экспоненциального закона распределения включают следующие: моделирование времени между отказами компьютерных систем, времени между приходом писем на почтовый сервер, времени ожидания пассажиров на автобусных остановках, времени между наступлением землетрясений и т.д.